main>
Motivation of introducing the invariant domain D.
The correspoinding problem for polynomial with 1 variable is very easy:
If W is a polynomial of 1 variable with positive coefficients containing
terms of degree 3 or higher, then W'(x)=x has exactly one positive solution.
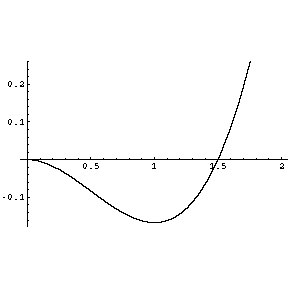 The Figure is a graph of y=w(x)=W(x)-x2/2 with
W(x)=x3/3.
The positive (x>0) critical point of w
(defined by w'(x)=0) is x=1.
Alternatively, one could of course also say that the unique fixed point
of the dynamical system on positive real axis
determined by a map grad W=W', is x=1.
The Figure is a graph of y=w(x)=W(x)-x2/2 with
W(x)=x3/3.
The positive (x>0) critical point of w
(defined by w'(x)=0) is x=1.
Alternatively, one could of course also say that the unique fixed point
of the dynamical system on positive real axis
determined by a map grad W=W', is x=1.
The motivation of Problem 1 is to extend this simple fact to
polynomials of 2 variables.
Note that for a polynomial in 2 variables with positive coefficients W,
the entire first quadrant
R+2={(x,y)|x>=0,y>=0} is
an invariant domain of grad W.
However, the uniqueness of the fixed points does not hold in general there.
As a subtle example, let
W(x,y;d) = x3 + x2y + d y3.
Then w(x,y;d)=W(x,y;d)-(x2+y2)/2 has
following critical points in the first quadrant for all d>0:
Furthermore, for d>=2/3:
| d>17/12 | d=17/12 | d<17/12 |
|---|
| No other solution | (3/13,2/13) |
2 other solutions |
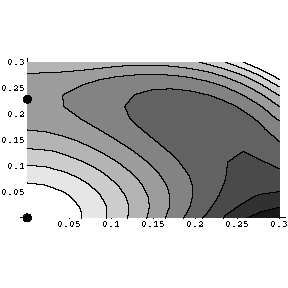
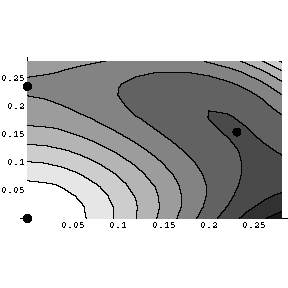
The Figures below are the contour plots of w(x,y;d) drawn by Mathematica.
The dots in the figures are the critical points of w (grad w=0).
d=17/12+0.04
d=17/12
d=17/12-0.04
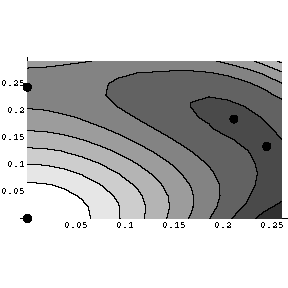
Here we see that as the coefficients in w is changed,
the critical points of w may appear/dissappear and bifurcate.
Such behaviors will totally ruin any general uniqueness conjecture.
For polynomials with 1 variable, positivity of coefficients for W was
a sufficient condition for the uniqueness.
We see that an appropriate choice of additional conditions
is important for W with 2 variables.
The domain D is not the only possible choice.
I have chosen D because the condition y<= x2
says that y is of "higher order" compared to x, if x is not large.
Hence I expect that things are qualitatively "similar" to the case of
1 variable in D, and the uniqueness of critical point will hold.
Certainly it must be a stronger condition than is necessary.
However, the subtleness of bifurcation of critical points
in the previous remark persuades me to think that we need conditions of
this strength to develop general theories.
main>

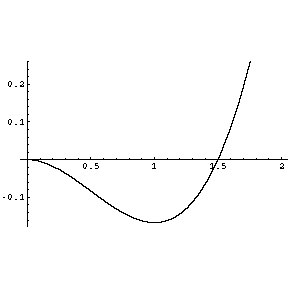 The Figure is a graph of y=w(x)=W(x)-x2/2 with
W(x)=x3/3.
The positive (x>0) critical point of w
(defined by w'(x)=0) is x=1.
Alternatively, one could of course also say that the unique fixed point
of the dynamical system on positive real axis
determined by a map grad W=W', is x=1.
The Figure is a graph of y=w(x)=W(x)-x2/2 with
W(x)=x3/3.
The positive (x>0) critical point of w
(defined by w'(x)=0) is x=1.
Alternatively, one could of course also say that the unique fixed point
of the dynamical system on positive real axis
determined by a map grad W=W', is x=1.


